こんにちは!たっきん(Twitter)です!
前回はOANDA APIとビジュアライズ化ライブラリのBokeh使って取得した為替レート値を使ってローソク足チャートを描写するプログラムを作りました。
今回はさらにテクニカル指標もいくつか描写してみましたので紹介したいと思います。
今回描写したテクニカル指標はこれです。
- 単純移動平均線
- MACD
- ボリンジャーバンド
どれもテクニカル指標の中でも人気が高いものをピックアップしました。
ちなみに、これらのテクニカル指標を計算するPythonライブラリとして、Pandasを使用しています。
テクニカル指標の計算式
まず最初に各テクニカル指標の計算式の説明と、コーディング方法を簡単に紹介していきます。
コードの出力結果は静的グラフになるように作ってみました!
単純移動平均線
単純移動平均線(Simple Moving Average:SMA)の計算式は至ってシンプルで、一定期間(\(n\)日間)の終値価格を平均するだけです。
\begin{align}
SMA_n &= \frac{1}{n}\sum_{j=1}^{n}{k_j}
\end{align}
\begin{align}
n &: 期間\\
k &: k-1期間前の終値
\end{align}
<サンプルコード>
import pandas as pd
import matplotlib.pyplot as plt
data = {"value": [120, 100, 90, 110, 150, 200, 300, 1000, 900, 800,
500, 300, 250, 200, 190, 150, 100, 50, 60, 80,
100, 150, 200, 400, 800, 1600]}
df = pd.DataFrame(data)
# --------------- n期間の移動平均線 ---------------
n1 = 3 # 期間の設定
n2 = 5 # 期間の設定
n3 = 10 # 期間の設定
SMAn1 = df["value"].rolling(window=n1).mean()
SMAn2 = df["value"].rolling(window=n2).mean()
SMAn3 = df["value"].rolling(window=n3).mean()
# ********** 描写 **********
fig1 = plt.figure("移動平均線")
plt.plot(df, label="Sample")
plt.legend()
plt.scatter(range(df.size), df)
plt.plot(SMAn1, linestyle="dashed", label="SMA-" + str(n1))
plt.plot(SMAn2, linestyle="dashed", label="SMA-" + str(n2))
plt.plot(SMAn3, linestyle="dashed", label="SMA-" + str(n3))
plt.legend()
plt.scatter(range(df.size), SMAn1, marker="*")
plt.scatter(range(df.size), SMAn2, marker="*")
plt.scatter(range(df.size), SMAn3, marker="*")
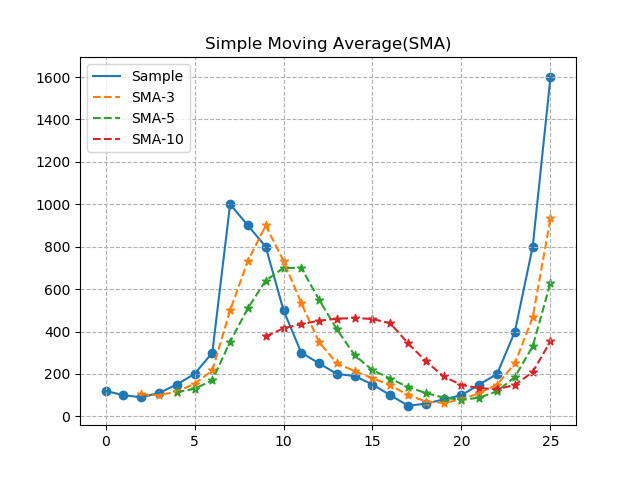
plt.title("Simple Moving Average(SMA)")
plt.grid(linestyle="dashed")
plt.show()<出力結果>
MACD
MACD(Moving Average Convergence and Divergence)もテクニカル指標の中では人気のあるうちの1つで、主にトレンド転換の判断に使われます!
計算式は以下のようになってます。
\begin{align}
MACD &= EMA_{sn} – EMA_{ln}\\
シグナル &= EMA_{mn}
\end{align}
\begin{align}
EMA_{sn} &: 移動平均のsn期間EMA\\
EMA_{ln} &: 移動平均のln期間EMA\\
EMA_{mn} &: MACDのmn期間EMA\\
※但し、&sn < ln を満たすこと
\end{align}
\(EMA\)は指数平滑移動平均線(Exponential Moving Average)を表しています。
\(EMA\)の計算式を説明すると長くなりそうなのでここでは割愛しますが、ググればたくさん出てくるので興味ある方は調べてみてください。
<サンプルコード>
import pandas as pd
import matplotlib.pyplot as plt
data = {"value": [120, 100, 90, 110, 150, 200, 300, 1000, 900, 800,
500, 300, 250, 200, 190, 150, 100, 50, 60, 80,
100, 150, 200, 400, 800, 1600]}
df = pd.DataFrame(data)
# --------------- MACD ---------------
sn = 3 # 移動平均(短期)期間の設定
ln = 7 # 移動平均(長期)期間の設定
mn = 5 # MACD期間の設定
EMAsn = df["value"].ewm(span=sn).mean()
EMAln = df["value"].ewm(span=ln).mean()
MACD = (EMAsn - EMAln)
SIGNAL = MACD.ewm(span=mn).mean()
# ********** 描写 **********
fig2 = plt.figure("MACD")
plt.plot(df, label="Sample")
plt.plot(MACD, linestyle="dashed", label="MACD")
plt.plot(SIGNAL, linestyle="dashed", label="Signal")
plt.legend()
plt.scatter(range(df.size), df)
plt.scatter(range(df.size), MACD, marker="*")
plt.scatter(range(df.size), SIGNAL, marker="*")
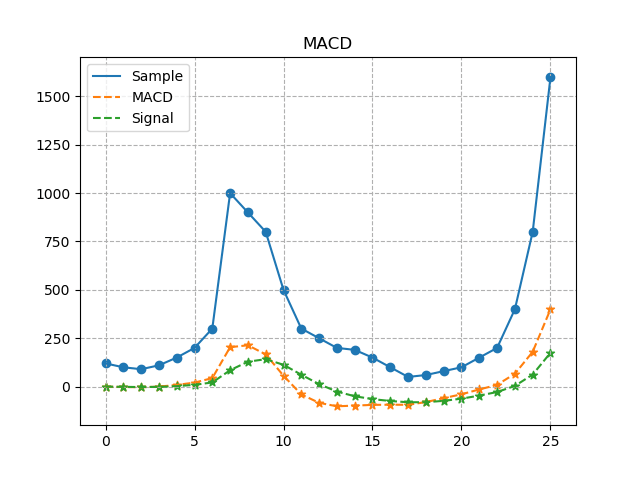
plt.title("MACD")
plt.grid(linestyle="dashed")
plt.show()<出力結果>
ボリンジャーバンド
ボリンジャーバンドも人気のテクニカル指標の1つですよね!
移動平均線と標準偏差によって形成された帯(バンド)の中に価格が納まる確率を算出することで、その後の価格推移を統計的に予想していくために利用されます。
で、その中心線と上下バンド線の計算式ですが、
<中心線>
\begin{align}
SMA_n
\end{align}
<上下バンド線>
\begin{align}
±1\sigma &= SMA_n ± \sigma_n\\
±2\sigma &= SMA_n ± \sigma_n × 2\\
±3\sigma &= SMA_n ± \sigma_n × 3\\
\end{align}
\(n\)は期間を表しています。
中心線は単純移動平均線ですね!
上下バンド線\(\sigma_n\)は\(n\)期間の標準偏差を表しています。
<サンプルコード>
import pandas as pd
import matplotlib.pyplot as plt
data = {"value": [120, 100, 90, 110, 150, 200, 300, 1000, 900, 800,
500, 300, 250, 200, 190, 150, 100, 50, 60, 80,
100, 150, 200, 400, 800, 1600]}
df = pd.DataFrame(data)
# --------------- ボリンジャーバンド ---------------
n = 5 # 期間の設定
# ===== 中心線の計算 =====
SMA_BB_n = df["value"].rolling(window=n).mean()
# ===== 上下バンド線の計算 =====
# 標準偏差の計算
sigma_n = df["value"].rolling(window=n).std(ddof=0)
# ±1σの計算
p1_sigma = SMA_BB_n + sigma_n
m1_sigma = SMA_BB_n - sigma_n
# ±2σの計算
p2_sigma = SMA_BB_n + sigma_n * 2
m2_sigma = SMA_BB_n - sigma_n * 2
# ±3σの計算
p3_sigma = SMA_BB_n + sigma_n * 3
m3_sigma = SMA_BB_n - sigma_n * 3
# ********** 描写 **********
fig3 = plt.figure("ボリンジャーバンド")
plt.plot(df, label="Sample")
plt.plot(SMA_BB_n, linestyle="dashed", label="SMA-" + str(n))
plt.plot(p1_sigma, c="hotpink", linestyle="dashed", label="+1σ")
plt.plot(m1_sigma, c="hotpink", linestyle="dashed", label="-1σ")
plt.plot(p2_sigma, c="aqua", linestyle="dashed", label="+2σ")
plt.plot(m2_sigma, c="aqua", linestyle="dashed", label="-2σ")
plt.plot(p3_sigma, c="lime", linestyle="dashed", label="+3σ")
plt.plot(m3_sigma, c="lime", linestyle="dashed", label="-3σ")
plt.legend()
plt.scatter(range(df.size), df)
plt.scatter(range(df.size), SMA_BB_n, marker="*")
plt.scatter(range(df.size), p1_sigma, marker="*", c="hotpink")
plt.scatter(range(df.size), m1_sigma, marker="*", c="hotpink")
plt.scatter(range(df.size), p2_sigma, marker="*", c="aqua")
plt.scatter(range(df.size), m2_sigma, marker="*", c="aqua")
plt.scatter(range(df.size), p3_sigma, marker="*", c="lime")
plt.scatter(range(df.size), m3_sigma, marker="*", c="lime")
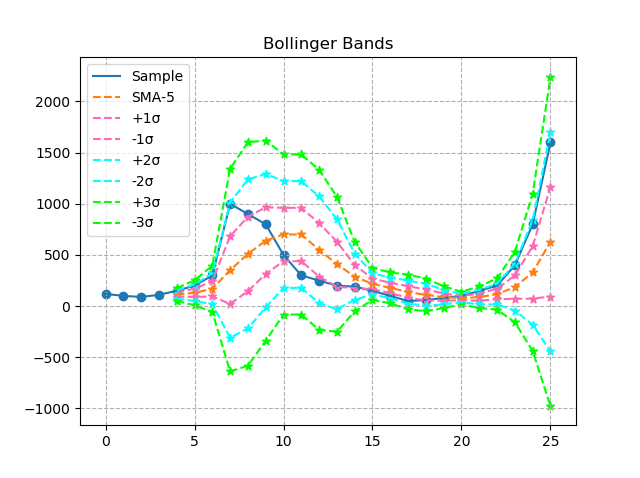
plt.title("Bollinger Bands")
plt.grid(linestyle="dashed")
plt.show()
<出力結果>
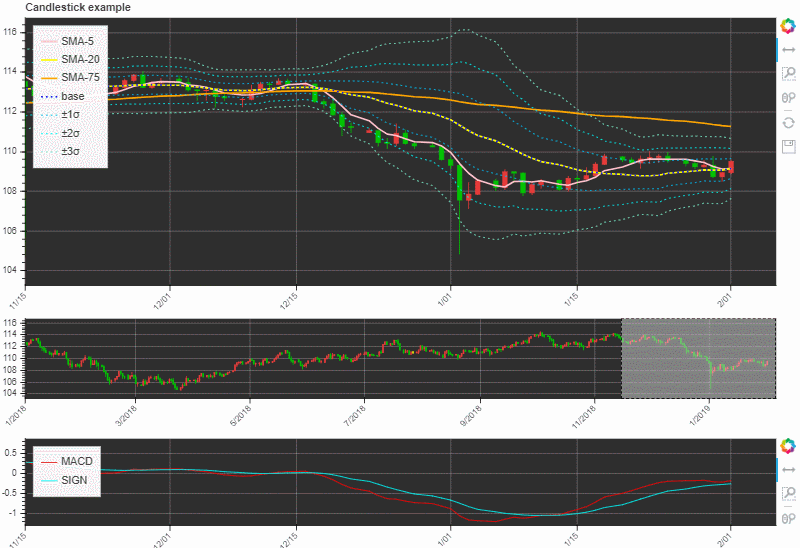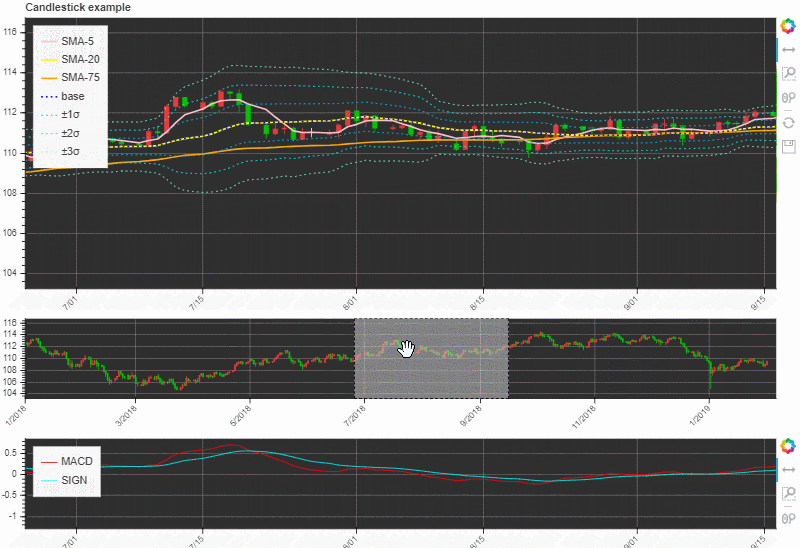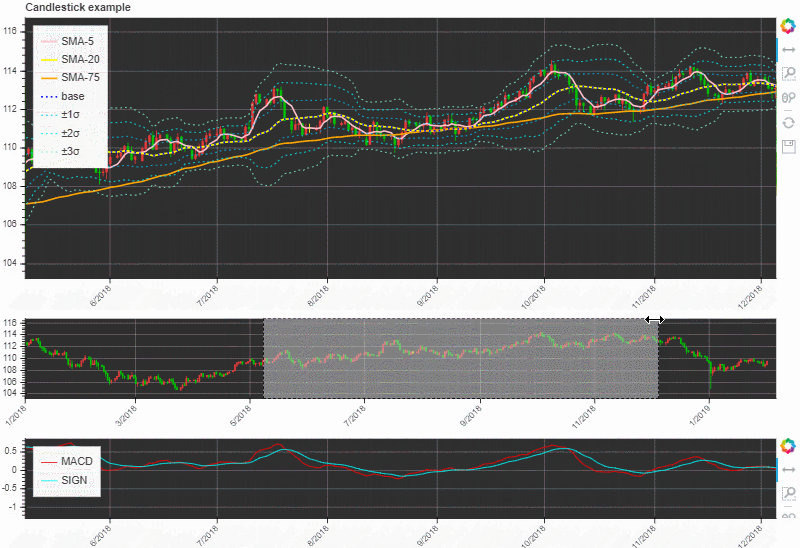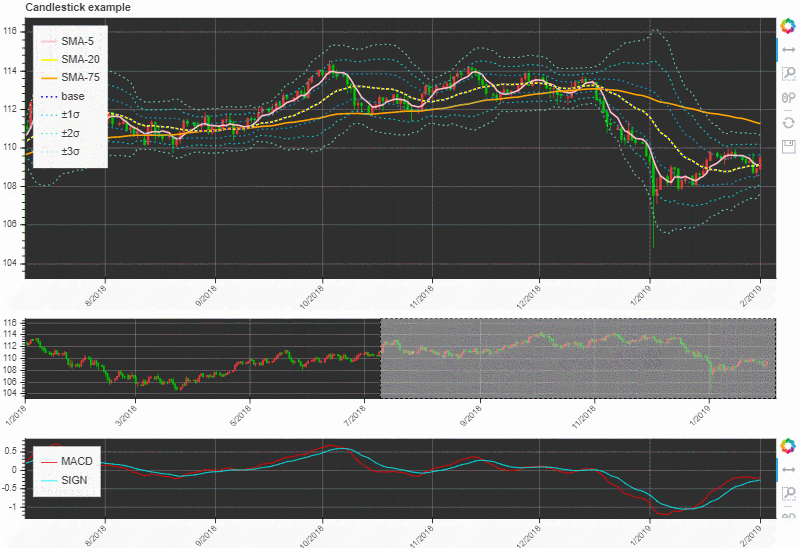
実際にBokehで描いてみた
以下のような動きになりました。
なんか取引ツールっぽい感じになってきましたね!
直接いじってみたい方は以下のhtmlファイルを開いてみてください!
ソースコード
今回作成したソースコードは全部GitHubで公開しています。
よかったら参考にしてみてください!
単純移動平均線、MACD、ボリンジャーバンドのサンプルコード
Bokehを使った描写





コメント